現今工業應用為了調控材料的性質,常會在將不同性質的材料混合,以構成複合材料(composite material),或是混成材料(hybrid material)。填充物的性質、尺寸、方向,其在基材中的分佈,均會影響整體材料性質,包括機械性質、熱力學性質、或是傳導率。複合或混成材料存在的形式有很多種,例如:將無機顆粒混入有機基材,以增強其機械性質或降低水份氣體的傳導率,可以製作保特瓶等食品包裝材料;調整非晶相(amorphous)基材中存在微晶粒的體積密度,控制材料導電度,即為相變化記憶體之運作原理。此外,調整共聚高分子(copolymer)或兩性分子(amphiphile)兩鍊段的長度及體積比,亦可得到不同微結構形式之混成材料。材料微結構,包括各成份之原性質與結構幾何特徵,決定其等效(effective)或外顯(apparent)性質,包括彈性模數等力學性質;熱傳導率、電傳導率、介電常數等傳導性質;以及受介面補捉效應影響的流體滲流率(fluid permeability)等。
複合或混成材料,一般而言,為一連續的基材(matrix)中存在著不連續的另一相,例如圓球、短柱等。但共聚高分子或界面活性劑也可能形成各種不同的微相分離結構,依其各成份間之相互溶解度及濃度比,依次為不規則、面心立方(FCC)、體心立方(BCC)、圓柱六角排列(Hex)、gyroid、層狀排列(Lam)等,如圖一。其中gyroid為一種雙連續相(bicontinuous phase)。雙連續相的形成,係由其組成份達到最低界面能時所造成的。以數學的觀點解析,可能存在的雙連續相有數百種。
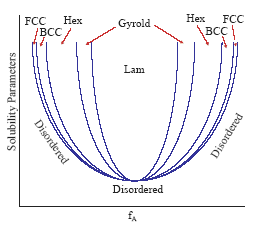
圖一、共聚高分子相圖
當連續相的傳導率遠低於不連續相時,傳導的路徑則為不連續相,故當不連續相之體積分率小時,無法構成一連通的傳導網絡。惟有當其體機積分率達一門檻值,混成材料整體的傳導率才開始大幅增加,此一現象,稱為滲漏(percolation)。然而,當連續相的傳導率遠高於不連續相時,傳導的路徑為連續相的基材,混成材料整體的傳導率大約可由其體積分率所決定,惟有當低傳導率的不連續相之體積分率超越某一門檻值,傳導率才開始大幅降低,對傳導產生阻絕的效果。下文簡介可用以計算複合材料傳導率的Bruggeman的等效介質方法,並進一步說明其於基材與顆粒之傳導率懸殊時的近似行為。此外,並以三維有限元素求取相變化記憶體材料之等效傳導率,以及非球狀顆粒對滲流的阻絕效果,期望對以微結構設計來控制材料傳導性質方面的應用,能有所幫助。
等效傳導率計算方法
對於幾種特殊微結構的異質二元複合材料的傳導性質,文獻中早有簡易的估計算式。例如Bruggeman即整理出複合材料傳導率之公式,可根據非晶相與結晶相之傳導率,計算非晶基材中存有部份結晶微區所構成複合材料之等效傳導率,同樣的計算公式,亦可用於等效熱傳導係數的計算。Bruggeman依結晶微區的幾何將傳導率公式分為四類:(1).當結晶微區為層狀,而電流方向與其垂直時;(2).結晶微區為層狀,而電流方向與其平行時;(3).結晶微區為許多隨機出現的平行柱狀,而電流方向與其軸心垂直時;(4).結晶微區為許多隨機出現的獨立球狀時,即可根據不同狀況求得其複合材料之等效傳導率。
等效的氣體或水份的滲流率估計
現假設一複合材料,其基材為高分子,加強材為如SiO2或clay等無機材料。高分子基材的氣體滲透率εa 比較高,無機加強材的氣體滲透率εc 比較低。假設二者的滲流率比值為 即 β,β=εc /εa,β<<1,依前述相同的推導方式,可依據當(1).無機加強材料的微結構為層狀,而氣體滲流方向與其垂直;(2).無機加強材料的微結構為層狀,或許多隨機出現的平行柱狀,而氣體滲流方向與其平行;(3).無機加強材料的微結構為平行橫向柱狀;(4).無機加強材料的微結構為許多隨機出現的獨立球狀等狀況下之等效滲流率的估計式。
相變化記憶體材料電導率之數值計算
前述的計算公式,適用於對由二種傳導率或滲透率相差很大之複合材料的等效性值作一快速的評估。然而,若要精確的預測複合材料的傳導率,則仍須經由數值計算。此處即介紹以有限元素計算相變化記憶體材料之等效電導率。相變化記憶體之記憶特性是由相變化材料之電阻值變化而定,相變化材料在非晶態有很高的電阻率,晶態有低佷多的電阻率;然而在相變化的過程中,晶態之體積分率是連續變化的,因此其電阻率也是連續變化的,也是造成元件SET與RESET之間電阻連續變化之原因。
圖二左側顯示三維有限元素模型,其中將一立方材料劃分為整齊的網格(mesh),利用亂數產生器選擇某些元素為結晶態,如圖中淺色的方格,而其他元素為非晶態,如圖中深色的方格。結晶態元素的電導率較高,即電阻率較低;而非晶態則正好相反。並在上下表面施加定額的電壓差,由計算所得電流量換算得整體之等效電阻率。圖二右側即為計算所得之電位等高線。圖三為結果與文獻相比較,圖中紅色三角形點即為有限元素模擬結果,實線與黑色方點為文獻實驗量測值,顯示二者數值十分吻合。

圖二、三維有限元素模型及計算所得之電位等高線

圖三、結晶相體積分率與電導率之關係
碟狀無機顆粒混成材料的氣體滲流率
塑膠材料被廣泛用來製成容器以盛裝液體,例如保特( PET )瓶。氣體於PET材料中尚具有相當的滲流率,如啤酒等飲料因其風味與所含氣體多寡相關,即不宜以一般PET瓶包裝。故有以分散之clay片材混於PET中構成奈米混成材料,以降低氣體滲流率的作法。其構想為藉由扁平狀的clay片材,增加氣體運動的路徑,而考量加工性,一般的添加量均在5%以下。由於clay為直徑厚度比很大的顆粒材料,直徑厚度比的高低,必然影響阻氣的效果。一般估計clay片材混高分子材料中的阻氣效果,以Nielsen公式最為簡易。圖四為三維FEM計算結果與Nielsen公式的比較。圖中方點與圓點分別為直徑厚度比約為19、49之等效滲流率計算結果;實線則為對應之Nielsen公式值。計算結果顯示:直徑厚度比越高者,等效滲流率越低,即阻氣果越好。但由片材所造成的幾何障礙,僅能降低等效滲流率數十個百分點,而無法有幾個數量級以上的降低效果。此外,Nielsen公式對於等效滲流率有明顯的低估。換言之,在以Nielsen進行clay阻氣效果評估時,應更為保守。
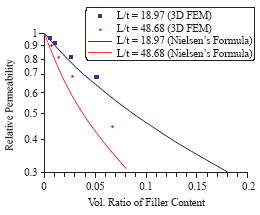
圖四、三維FEM計算結果與Nielsen公式的比較
作者:邱佑宗、葉吉田 / 工研院材化所
出處:工業材料雜誌255期
★詳全文:https://www.materialsnet.com.tw/DocView.aspx?id=6712