大數據與機器學習都是數據科學( Data Science ),如果能將材料科學結合數據科學,從既有的實驗數據中找出規律或趨勢,做為新型材料分子的設計依據,不僅可以降低人為主觀的判斷誤差,更可以加速新材料的開發時程。
目前大家所稱的大數據( Big Data ),從數據的儲存、處理,到模型設計、趨勢預測一概囊括,但是後段的物理模型設計、數據趨勢的預測及分類,其更偏向於資料探勘及機器學習的範疇,從廣義來看,更是牽扯到人工智慧(AI)的領域。
機器學習( Machine Learning )是人工智慧的一個分支,機器學習可以根據選用不同的演算法或數學模型,從人為給定的過去經驗「訓練資料集( Training Set )」進行「學習( Learning )」,自動分析以獲得規律,並且利用此規律對未知的新資料進行預測;當有新的訓練資料進入時,重複「學習」的過程,可重新獲得規律。因此以下針對幾種常見的機器學習演算法進行介紹,並輔以實例說明。
演算法簡介與材料科學之應用
1. 最小平方法
最小平方法(Least Squares Regression)是迴歸分析最常用的方法之一。在材料領域中,迴歸分析是用來剖析實驗數據常用的方法,藉以歸納出所謂的半經驗公式(Semi-empirical Equation)。例如QSAR模型(Quantitative Structure–Activity Relationship Models)或基團貢獻法(Group Contribution Methods)皆是透過迴歸分析方式,歸納出材料分子的規律,進一步做為新材料物性預測的依據。
3. 支持向量機
支持向量機( Support Vector Machines; SVM )是一種將數據分類用的演算法,由 Corinna Cortes及Vladimir Vapnik 根據統計學習理論於1995年所提出。支持向量機在解決小的訓練資料集、非線性以及高維度問題中表現出許多的優勢,是目前廣受使用的一種統計分類演算法。
支持向量機主要的概念是找出一個n-1維的超平面( Hyperplane ),使超平面在n維的系統中將訓練資料「分類」為兩組不同群體;如圖六,有一組二維的訓練資料被一維的超平面區分類為A、B兩組群體。超平面的數學形式如式(5)所示。
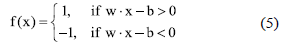
其中x是輸入值;w是垂直於超平面的向量或稱為支持向量( Support Vectors );b則是位移( Offset )。以圖六的二維系統來說,其實能畫出無限多個超平面,而最佳的超平面要距離訓練資料點越遠越好,避免因為計算精度造成誤判,換句話說,最佳的超平面應該擁有最長的支持向量。
圖六、二維訓練資料(X1, X2)被一維的超平面(虛線)分類為A、B兩組代表不同的輸出值(組別),實線是資料到超平面的法線向量,即是支持向量
5. 群集分析
群集分析將數據依其相似的程度劃分成數個群。在階層式( Hierarchical )群集分析過程中,首先將每一個數據各自視為一個群,並計算與其他群之間相似性。再將最相似的二個群合併為一個群。重複此步驟直到所有的數據都合併在一個群中。以下用影像分析為案例,說明群集分析的功能。圖十四(a)的影像中共有26個編號的白色顆粒,可用階層式群集分析將其區分為數個群。輸入的資料為…以上為部分節錄資料,完整內容請見下方附檔。
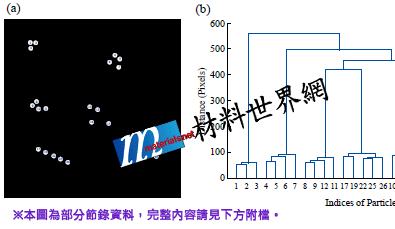
圖十四、(a)內含26個白色顆粒的影像;(b)群集分析產生的樹狀圖
作者:張哲銘、闕銘宏、陳立基 / 工研院材化所
★本文節錄自「工業材料雜誌」361期,更多資料請見下方附檔。